49. ročník matematickej olympiády 1999-2000 | |||||
| Z4 | Z5 | Z6 | Z7 | Z8 | Z9 |
| 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo |
| 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo |
| 3. kolo | |||||
Z4-I-1
Keď mala mamička upečených 25 palaciniek, začali deti jesť. Kým mamička upečie dve palacinky, deti stihnú tri zjesť. Deti zjedli 27 palaciniek, povedali, že im už stačilo, a mamička prestala piecť. Koľko palaciniek zvýšilo pre mamičku a pre otecka?
Z4-I-2
Nahraď hviezdičky číslicami tak, aby súčet výsledkov obidvoch príkladov bol 18 210.
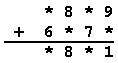 | 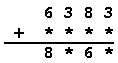 |
Z4-I-3
Tomáško dostal zahraničnú čokoládu. Postupne si z nej odlamoval kúsky – vždy len celý riadok alebo stĺpček. Prvý kúsok vážil 18 gramov, druhý 9 gramov a tretí 15 gramov.
Nakresli si malý obdĺžnik – to bude jeden dielik čokolády.
A teraz nakresli celú čokoládu a jednotlivé kúsky, ktoré Tomáško odlomil. Ku každému oz obrázkov dopíš, koľko "váži".
Z4-I-4
Dnes ráno kúpil Peter vo veľkosklade 125 malinoviek. Za každú z nich zaplatil 7 Sk. Tieto malinovky predával na kúpalisku po 10 Sk a prázdne fľaše vykupoval po 3 Sk za kus. V priebehu dňa Peter dve malinovky vypil, jednu vylial a dve rozbil, zvyšok sa mu podarilo predať. Večer odniesol 25 prázdnych fliaš do veľkoskladu, viac sa mu ich nevrátilo. Vo veľkosklade mu za každú z nich vyplatili 2 Sk. Koľko si Peter zarobil?
Z4-I-5
Doplň do tabuľky chýbajúcich 5 čísel, ak vieš:
Všetky čísla v tabuľke sú navzájom rôzne. Súčet čísel v každom riadku i stĺpci má byť rovnaký a čo najmenší. Vysvetli, prečo tvoj súčet nemôže by menší.
| 3 | ||
| 8 | 2 | |
| 7 |
Z4-I-6
V jedálni upiekli koláč a rozrezali ho na štvorce 4 x 4 cm. Aby sa jednotlivé kusy nepolepili, ukladali ich tak, aby medzi nimi ostávali medzery široké 1 cm. Na malú štvorcovú tácku sa takto zmestili 4 a pri okrajoch neostalo žiadne voľné miesto. Narysuj túto tácku aj s koláčmi na štvorčekový papier. Koľko koláčov by sa vmestilo na veľkú tácňu s 11-násobnými rozmermi?
| hore |
 Z4-II-1
Z4-II-1
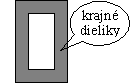
Ondrej a Zuzka dostali spoločnú maxičokoládu. Ondrej z nej jedol prvý a zjedol všetky "krajné" dieliky. Zuzke takto zostalo 15 dielikov. Koľko dielikov mala maxičokoláda? Kto zjedol viac čokolády, Ondrej alebo Zuzka? O koľko dielikov?
Z4-II-2
Do krúžkov doplň celé čísla, aby platili naznačené matematické operácie, a tretie najmenšie číslo bolo 315.
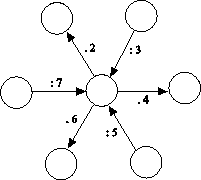
Z4-II-3
Pán Strúčik sadí fazuľu pekne do riadkov. Dva susedné riadky sú od seba vždy rovnako ďaleko, presne 30 cm. V každom riadku je 36 fazuliek a dve susedné fazuľky sú vo vzdialenosti 4 cm od seba. 86 fazuliek zasadil pán Strúčik vo vzdialenosti 5 cm od okraja záhona, zvyšných 238 bolo od okraja ďalej.
Koľko riadkov fazule vysadil pán Strúčik? Aké rozmery má jeho fazuľový záhon?
| hore |
Z5-I-1
V príkladoch:
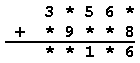 |
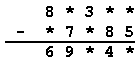 |
nahraďte hviezdičky číslicami tak, aby jeden výsledok bol o 15 764 väčší ako druhý.
Z5-I-2
V našej dedinke žije približne (zaokrúhlené na desiatky) 240 ľudí. Modrookých ľudí je v nej presne 8-krát menej ako tých, ktorí modré oči nemajú. Koľko obyvateľov našej dedinky má modré oči? Koľko je tých, čo majú oči inej farby?
Z5-I-3
Jeden z troch štvorcov, na ktoré sme rozdelili obdĺžnik má obsah 36 cm2. Aké rozmery mohol mať obdĺžnik?
Z5-I-4
Doplň v tejto tabuľke čísla tak, aby sa súčet ľubovolných troch susedných čísel v riadku aj stĺpci rovnal 123.
| 29 | |||
| 56 | |||
| 13 | |||
| 18 |
Z5-I-5
Adam zložil zo 6 paličiek rovnostranný trojuholník. Potom jednu paličku stratil a zostali mu len paličky s dĺžkami 25, 29, 33, 37 a 41 cm. Akú dĺžku mohla mať palička, ktorú Adam stratil?
Aby Adam mohol poskladať rovnostranný trojuholník aj bez chýbajúcej paličky, musí jednu zo zvyšných rozlámať. Ktorú paličku a na ako dlhé časti? Podarilo by sa mu to aj vtedy, keby šikovne rozlámal nejakú inú?
Z5-I-6
Včera dostal Andrejko od mamičky 17 lentiliek, dnes o 6 viac. Včera zjedol o 4 lentilky menej ako dnes. Teraz má 8 lentiliek. Koľko lentiliek zjedol dnes a koľko včera?
| hore |
Z5-II-1
Jurko požičal predvčerom Miškovi približne (zaokrúhlené na desiatky) 230 Sk, včera ďalších približne 180 Sk. Miško mu dnes vrátil približne 420 Sk a teraz mu dlhuje už len 3 koruny. Vieš presne koľko korún si požičal Miško od Jurka včera a koľko predvčerom? Požičiaval si aj vracal len celé koruny, žiadne haliere!
Z5-II-2
Vojto má dva obdĺžniky. Prvý z nich má šírku 7 cm a dĺžku 11cm, druhý má rozmery 8 cm a 4 cm. Aké obvody môžu mať šesťuholníky z nich zložené? Pozor, obdĺžniky sa nesmú prekrývať!
Z5-II-3
Milanko rád počíta s kalkulačkou. Včera na nej počítal príklad 23 + 19 . 56. Zabudol však, že jeho kalkulačka neuprednostňuje násobenie pred sčítaním. Aký výsledok mu vyšiel? Aký je správny výsledok? Dnes mal Milanko k číslu 75 pripočítať niekoľkonásobok čísla 41. Znovu použil kalkulačku, urobil tú istú chybu ako včera a vyšiel mu nesprávny výsledok 3813. Aký príklad mal Milanko počítať a aký je jeho správny výsledok?
| hore |
Z6-I-1
V príkladoch:
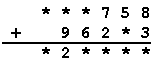 |
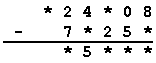 |
nahraďte hviezdičky správnymi ciframi tak, aby výsledok jedného príkladu bol 7-krát väčší než výsledok druhého príkladu.
Z6-I-2
Rozdeľte štvorec so stranou dĺžky 12 cm na tri obdĺžniky s rovnakými obvodmi tak, aby tieto obvody boli čo najmenšie.
Z6-I-3
V cukrárni Sladký svet predávajú malú tridsaťgramovú a veľkú stogramovú čokoládu JÚLIA. Malá JÚLIA stojí 7 Sk a veľká 24 Sk.
a) Koľko najmenej korún musí mať babička, aby mohla svojim vnúčatám kúpiť 750 g čokolády JÚLIA?
b) Aké najväčšie množstvo tejto čokolády môže babička kúpiť, keď má len 110 Sk?
Z6-I-4
Mamička priniesla z obchodu krabicu kockového cukru. Betka zjedla najprv celú "hornú vrstvu", teda 77 kociek cukru, potom jednu "bočnú vrstvu", kde bolo 55 kociek cukru, a nakoniec "prednú vrstvu". Koľko kociek cukru ešte zostalo v krabici?
Z6-I-5
Myslím si štvorciferné číslo. Poradím ti, že súčet prvých dvoch číslic je 3, súčet posledných dvoch je 7 a prostredné dvojčíslie sa dá deliť 4 bezo zvyšku. Aké si môžem myslieť číslo? Nájdi všetky možnosti.
Z6-I-6
Sedem trpaslíkov chcelo urobiť Snehulienke radosť, a preto jej kúpili krásne obdĺžnikové zrkadlo. Cestou boli neopatrní a rozbili ho na štyri trojuholníkové časti presne tak, ako je to znázornené na obrázku. Trpaslíci chceli zrkadlo opraviť, ale nikomu sa to nepodarilo. Každý zložil iné štvoruholníkové zrkadlo. Nakresli zrkadlá, ktoré poskladali trpaslíci.

| hore |
Z6-II-1
Snehulienka a 7 trpaslíkov cestovali navštíviť kamarátku Ruženku Šípkovú. Tam cestovali vlakom, naspäť sa vracali autobusom. Snehulienka si musela kúpiť celý lístok, trpaslíci našťastie mohli cestovať za polovičné cestovné. Cesta tam a späť ich všetkých vyšla na 729 korún. Celý lístok na vlak stojí 78 korún. Koľko korún stojí celý lístok na autobus?
Z6-II-2
Šesťuholník načrtnutý na obrázku sa dá rozdeliť na dva rovnaké obdĺžniky (dĺžky strán šesťuholníka vyjadrené v cm sú celé čísla). Obsah šesťuholníka je 48 cm2, jeho obvod sadá deliť 4 bezo zvyšku. Urči rozmery obdĺžnikov.
Z6-II-3
Miško a Ferko striedavo hádžu guľôčky do jamky. Každá štvrtá Miškova a každá piata Ferkova guľôčka skončí v jamke. Teraz je v jamke 17 guľôčok. Koľko guľôčok je okolo jamky?
| hore |
Z7-I-1
V príkladoch:
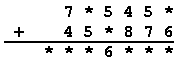 |
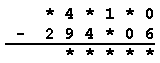 |
nahraďte hviezdičky správnymi ciframi tak, aby výsledok jedného príkladu bol 23-krát väčší než výsledok druhého príkladu.
Z7-I-2
Dvorného matematika sa spýtali na jeho zárobok za minulý mesiac. Odpovedal takto: "Ak pripočítame k číslu odpovedajúcemu mojej výplate v korunách všetky čísla, ktoré dostaneme z pôvodného čísla zámenou poradia jeho cifier, vyjde nám číslo 4218. Zárobok mi vyplatili čo najmenším počtom jednokorunových mincí, desaťkorunáčok a stokorunáčok." Koľko "kusov" peniazov matematik dostal? Koľko najmenej a koľko najviac korún si mohol matematik zarobiť?
Z7-I-3
Obdĺžnik a trojuholník majú rovnaké obvody. Všetky dĺžky ich strán sú vyjadrené dvojcifernými číslami. Čísla sa nám "zosypali" z obrázka na jednu hromadu a vznikla z nich táto skupina cifier:
0 1 1 1 1 1 2 3 4 4 4 5 6 6.
Aké mohli byť pôvodné rozmery oboch útvarov? Nájdi aspoň tri riešenia.
 Z7-I-4
Z7-I-4
Paľko nafarbil troma farbami steny kvádra – dvojice protiľahlých rovnakou farbou. Potom začal odvaľovať kváder po papieri. Vznikla takáto stopa (obrázok):
Zisti rozmery kvádra, ak vieš, že zafarbená plocha je štvorec o obsahu 36 cm2.
(Úloha má viac riešení.)
Z7-I-5
Z obdĺžnika sme odstrihli 11/16 jeho obsahu. Ostal nám útvar zakreslený na obrázku. Aké rozmery mohol mať pôvodný obdĺžnik?

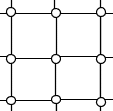
Z7-I-6
Je daných 9 bodov štvorcovej siete (obrázok). Nájdi všetky rôzne nezhodné trojuholníky s vrcholmi v týchto bodoch. Potom týmito trojuholníkmi pokry celú plochu štvoruholníka na obrázku. (Trojuholníky sa nesmú prekrývať.)
 |
 |
| hore |
Z7-II-1
Doplňte tabuľku tak, aby súčet čísel v každom štvorci 2 x 2 bol rovnaký.
| 1 | 4 | ||
| 6 | 7 | ||
| 3 | 2 | ||
| 8 | 5 |
Z7-II-2
Jakub chcel oblepiť povrch svojej drevenej kocky nálepkami. V obchode mali dva druhy tvaru rovnoramenného trojuholníka. Červené mali základňu rovnako dlhú ako je dĺžka hrany kocky a výšku tak dlhú ako 1,5 dĺžky hrany kocky. Modré mali základňu trikrát dlhšiu ako je dĺžka hrany kocky a výšku tak dlhú ako polovica dĺžky hrany kocky. Koľko červených a modrých nálepiek musel Jakub kúpiť, aby oblepil celý povrch kocky? (Nálepky sa nesmú strihať.)
Z7-II-3
Dávid pri sčítaní vždy zabudne pri prechode cez desiatku pripočítať jednotku. Tú istú chybu robí aj pri odčítaní. V poslednej písomke mu vyšiel súčet dvoch čísel 5819. Urobil skúšku odčítaním a vyšiel mu správny výsledok 2843 (t.j. skúška mu vyšla). Aký príklad Dávid počítal a aký súčet mu mal vyjsť.
| hore |
Z8-I-1
Kráľovská loď viezla 100 truhličiek. Vo všetkých bol rovnaký počet perál. V prvom prístave piráti tajne odobrali z 1. truhličky niekoľko perál. Nikto nič neodhalil, a tak v druhom prístave piráti odobrali z druhej truhličky dvakrát toľko perál ako predtým z prvej. Opäť nikto nič neodhalil. V treťom prístave piráti zobrali z 3. truhličky trikrát toľko ako z prvej. A tak to išlo ďalej, až po poslednom odobratí v stej truhličke ostala už len jedna perla. Loď doviezla do cieľa iba 24 850 perál. To už sa všetko prezradilo a pirátov chytili. Pre stanovenie výšky trestu a náhradu škody bolo treba zistiť, koľko perál bolo v truhličkách pôvodne. Koľko?
Z8-I-2
Daný je štvorec ABCD a bod P tak, že D je stred úsečky AP. Bodom P prechádza priamka p. Táto delí štvorec na dva útvary, ktorých obsahy sú v pomere 5 : 3. Narysujte priamku p.
Z8-I-3
Myslím si číslo. Zámenou poradia jeho cifier viem vytvoriť ďalších 5 čísel. Ak ich všetky pripočítam k pôvodnému číslu, vyjde mi 4 218. Moja kamarátka Monika si myslí číslo o 5 väčšie. Keď k nemu pripočíta všetky čísla získané zámenou poradia jeho cifier dostane súčet 5 328. Aké číslo si myslím ja a aké Monika?
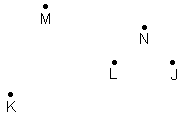
Z8-I-4
Na obrázku sú dané body J, K, L, M, N. Zostrojte rovnoramenný
trojuholník ABC so základňou AB, ak vieme, že body J, K, L, M, N ležia po rade na priamkach AC, vc, va, vb, tc.
Z8-I-5
Nájdite štvorciferné čísla delitelné 7, pre ktoré platí:
súčet prvých dvoch cifier je 10,
súčet prostredných dvoch cifier je 10,
súčet posledných dvoch cifier je 9.
Z8-I-6
Na každej stene 17-bokého ihlana je napísané číslo. Súčet všetkých týchto čísiel je 96. Každý vrchol má priradené číslo získané sčítaním čísel na všetkých stenách, ktoré tento vrchol obsahujú. Zistili sme, že všetky vrcholy majú priradené rovnaké číslo. Aké čísla sú na stenách?
| hore |
Z8-II-1
Násobením dvoch dvojciferných čísel dostaneme 2 176. Ak zameníme poradie číslic v oboch činiteľoch, bude súčin 1 978. Aké sú to čísla?
Z8-II-2
V trojuholníku ABC je strana AC dlhšia ako strana BC. Ťažnica CS a výška CP delia uhol ACB trojuholníka ABC na tri zhodné uhly. Úsečka SZ je výška trojuholníka ASC. Vypočítajte obsah trojuholníka ABC, ak viete, že obsah trojuholníka ASZ je 9 cm2. (Body S, P, Z ležia na stranách trojuholníka ABC.)
Z8-II-3
Pohyblivé schody vyvezú človeka nahor za 12 sekúnd. Miško po susedných nepohyblivých schodoch vybehne hore za 6 sekúnd. Za ako dlho by sa dostal Miško hore, keby bežal rovnako rýchlo ako predtým, ale po pohyblivých schodoch?
| hore |
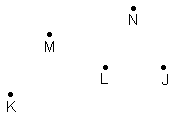
Z9-I-1
Na obrázku sú dané body J, K, L, M, N. Zostrojte pravouhlý trojuholník ABC s preponou AB ak viete, že body J, K, L, M, N ležia po rade na priamkach AB, BC, CA, vc, vc.
Z9-I-2
Nájdite štvorciferné číslo abcd s ciframi a, b, c, d, pre ktoré platí:
ab : bc = 1 : 3
bc : cd = 2 : 1
(ab, bc, cd sú dvojciferné čísla s ciframi a, b, c, d.)
Z9-I-3
Polpriamky AX a BY rozdeľujú uhly CAB a ABC trojuholníka ABC v pomere 1 : 2 a pretínajú sa v strede kružnice opísanej trojuholníku ABC. Určite uhly tohto trojuholníka.
Z9-I-4
V Kocúrkove haliere nemajú. Zato tam majú takýto stroj na zamieňanie mincí za papierové bankovky. Najprv sa celá vhodená suma zaokrúhli na desiatky. Takto získaná hodnota sa zaokrúhli na stovky. A potom ešte na tisícky. Výsledná suma sa vydá v bankovkách. Jano sa rozčuľoval, že ho kocúrkovský zamieňací stroj poriadne dobehol. Nasypal doň odrazu celý svoj majetok a on mu vydal len približne 69% (zaokrúhlené na celé percentá) toho, čo doň vhodil. Koľko Kocúrkovských korún doň mohol nasypať?
Z9-I-5
Šesťsten ABCD vznikol zlepením štvorstenov ABCD a ABCE. Na každej jeho stene je napísané číslo. Každý vrchol má priradené číslo získané sčítaním čísel na všetkých stenách, ktoré tento vrchol obsahujú. Nájdite všetky také očíslovania stien, pre ktoré sú všetkým vrcholom priradené rovnaké čísla, ak viete, že dve susedné steny majú čísla 4 a 9. Susedné steny majú spoločnú jednu hranu telesa.
Z9-I-6
Vo vrcholoch štvorca sú napísané čísla 1, 2, 3, 4. Paľo menil čísla vždy v niektorej trojici susedných vrcholov takto: Buď vo všetkých troch zväčšil ich číslo o 1, alebo vo všetkých troch zmenšil ich číslo o 1. (obrázok 2)
| obr. 2 | 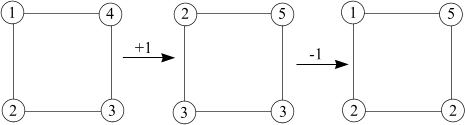 |
a) Môže popísanými operáciami dostať štvorec so samými štvorkami?
b) Ktoré z nasledujúcich obrazcov možno uvedeným spôsobom premeniť tak, ako je to znázornené na obrázkoch 3, 4 a 5? (Prečo?)
| obr. 3 | 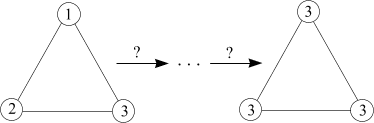 |
| obr. 4 | 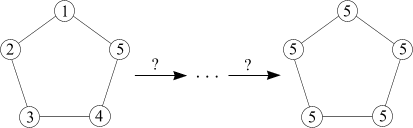 |
| obr. 5 | 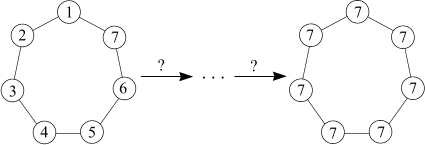 |
| hore |
Z9-II-1
Napíšme za sebou čísla 2000, 1999, 1998, ... 3, 2, 1 (bez čiarok). Medzi ne umiestnite znaky + a -. Vznikne tak príklad s 1999 počtovými operáciami. Aké najmenšie prirodzené číslo takto môžeme dostať? Svoje riešene vysvetlite.
Z9-II-2
Zostrojte trojuholník ABC, ak je daný stred S kružnice jemu opísanej, stred D strany AB a ťažisko T (obrázok).
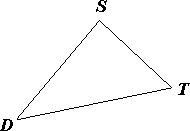
Z9-II-3
Nájdite všetky celé čísla a, b, pre ktoré platí:
a + zao10(a) = zao100(a)
b + zao10(b) + zao100(b) + zao1000(b) = 2764
zao10(x) je číslo x zaokrúhlené na desiatky.
zao100(x) je číslo x zaokrúhlené na stovky.
zao1000(x) je číslo x zaokrúhlené na tisícky.
Z9-II-4
Polpriamky AX a BY rozdeľujú uhly CAB a ABC trojuholníka ABC v pomere 1 : 2 a pretínajú sa v priesečníku jeho výšok. Určite uhly tohto trojuholníka.
| hore |
Z9-III-1
Janko si myslel dve dvojciferné čísla. Erikovi prezradil, že jedno získa zámenou cifier druhého a ich rozdiel je 3/4 menšieho z nich. Erik po krátkom počítaní povedal, že také čísla pozná. Ktoré čísla si Janko mohol myslieť?
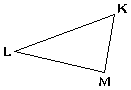
Z9-III-2
Daný je trojuholník KLM. Zostrojte rovnoramenný trojuholník ABC, s ramenami AC a BC, ak viete, že body K, L sú päty výšok trojuholníka ABC na jeho ramená a bod M leží na priamke AB. Urob rozbor a konštrukciu.
Z9-III-3
Nájdite všetky trojciferné čísla x, ktoré sa po zaokrúhlení na stovky rovnajú číslu ![]() .
.
Z9-III-4
Šesťsten ABCDE vznikol zlepením štvorstenov ABCD a ABCE. Na každej jeho stene je napísané nenulové číslo. Každý vrchol má priradené číslo získané súčinom čísel na všetkých stenách, ktoré tento vrchol obsahujú. Nájdite všetky také očíslovania stien, pre ktoré sú všetkým vrcholom priradené rovnaké čísla, ak viete, že dve steny majú čísla 4 a 44.
| hore |