49. ročník matematickej olympiády 1999-2000
| C | B | A |
| domáce kolo | domáce kolo | domáce kolo |
| školské kolo | školské kolo | školské kolo |
| krajské kolo | krajské kolo | krajské kolo |
| celoštátne kolo | ||
C-I-1
Pri delení istého prirodzeného čísla číslami 19 a 99 dostaneme ako zvyšky dve prvočísla. Súčet oboch neúplných podielov sa rovná 1999. Určte delené číslo.
C-I-2
Nájdite všetky pravouhlé trojuholníky, v ktorých spojnica stredov vpísanej a opísanej kružnice zviera s preponou uhol 45°.
C-I-3
Zistite najmenšie prirodzené číslo k, pre ktoré platia jednotlivé tvrdenia a), b), c).
Ak obsadíme figúrkami ľubovoľných k polí šachovnice 8 x 8, budú
obsadené niektoré
a) tri susedné polia niektorého riadku,
b) tri susedné polia niektorého šikmého riadku,
c) štyri susedné polia niektorého riadku alebo stĺpca.
Šikmým radom rozumieme takú skupinu polí, ktorých uhlopriečky jedného z oboch smerov ležia na jednej a tej istej priamke.
C-I-4
Juro zhotovil papierový model pravidelného štvorbokého ihlana ABCDV s podstavou ABCD. Keď potom model rozrezal pozdĺž štyroch hrán, bolo ho možné rozvinúť (bez prekrytia) do roviny. Koľko rôznych sietí daného ihlana tak mohol Juro dostať? Ukázalo sa, že sieť, ktorú Juro dostal, mala tvar (nekonvexného) sedemuholníka. Vypočítajte uhol AVB v bočnej stene ihlana.
C-I-5
V číselnom výraze
+ 1 + 2 + 3 - 4 - 5 - 6 + 7 + 8 + 9 - 10 - 11 - 12 + ... + 595 + 596 + 597 - 598 - 599 - 600 ),
v ktorom chýba ľavá zátvorka, sú postupne vypísané všetky prirodzené čísla od 1 do 600; pred nimi sa pravidelne opakujú tri znamienka + a tri znamienka -. Doplňte ľavú zátvorku do výrazu tak, aby vyšiel výsledok 378.
C-I-6
Daný je pravidelný šesťuholník KLMNOP. Zostrojte pravouhlý trojuholník ABC s preponou AB tak, aby jeho vrchol C ležal na úsečke NP, body M, O, K ležali po rade na priamkach AB, BC, CA a aby priamka NP rozdelila trojuholník ABC na dve časti s rovnakým obsahom.
| hore |
C-S-1
Nájdite najmenšie prirodzené číslo k, pre ktoré platí: Ak vyberieme ľubovoľných k rôznych čísel z množiny {1, 4, 7, 10, 13, ..., 1999}, potom medzi vybranými existujú dve rôzne čísla, ktorých súčet sa rovná 2000.
C-S-2
Štvorec ABCD a obdĺžnik AEFD majú takú vzájomnú polohu, že bod B leží na kružnici vpísanej trojuholníku AEF. Vypočítajte pomer dĺžky a šírky obdĺžnika AEFD.
C-S-3
Ak celé kladné číslo N vydelíme číslom 19 a získaný neúplný podiel ďalej vydelíme číslom 99, vyjde nám pri druhom delení rovnaký neúplný podiel a rovnaký zvyšok, ako keď pôvodné číslo N vydelíme číslom 1999. Určte ako najmenšie, tak aj najväčšie také číslo N.
| hore |
C-II-1
Z dreva je vyrobených šesť zhodných pravidelných štvorbokých ihlanov a kocka. Stena kocky je zhodná s podstavami ihlanov. Určte pomer povrchu kocky a telesa, ktoré vznikne zlepením podstáv ihlanov so stenami kocky, ak je pomer objemov týchto telies 1:2.
C-II-2
Milan zapísal za seba niekoľko prvých prirodzených čísel, vynechal pri tom len čísla 4, 9, 14, 19, 24, 29, ... Potom medzi zapísané čísla vpísal striedavo znaky mínus a plus, takže dostal výraz
1 - 2 + 3 - 5 + 6 - 7 + 8 - 10 + 11 - 12 + 13 - 15 + ...
Nakoniec ešte vpísal ľavú zátvorku za každý znak mínus a rovnaký počet pravých zátvoriek zapísal až na koniec výrazu:
1 - (2 + 3 - (5 + 6 - (7 + 8 - (10 + 11 - (12 + 13 - (15 + ...))))))
Výsledný výraz mal hodnotu 103. Koľko čísel bolo v Milanovom výraze? (Zistite všetky možnosti.)
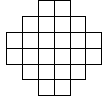
C-II-3
Aký najväčší počet figúrok je možné rozostaviť na jednotlivé polia hracej dosky z obrázku tak, aby v žiadnom šikmom rade neboli figúrkami obsadené žiadne tri susedné polia? Nezabudnite zdôvodniť, prečo väčší počet figúrok takto rozostaviť nemožno. (Šikmým radom rozumieme takú skupinu polí, ktorých uhlopriečky jedného z oboch smerov ležia na jednej priamke.)
C-II-4
V rovine sú dané body A, L, M také, že |AL| = 6,3 cm, |LM| = 5,6 cm, |LM| = 1,8 cm. Zostrojte lichobežník ABCD, ktorému sa dá vpísať kružnica, ktorá sa dotýka ramena BC v bode M (body dotyku so základňou AB a ramenom AD lichobežníka ABCD nie sú dané).
| hore |
B-I-1
Pre ktoré reálne čísla t má funkcia f(x) = 5x + 44 + t.|x - 2| - 3.|x - t| maximum rovné 0?
B-I-2
Označme S stred kružnice vpísanej ľubovoľnému trojuholníku ABC. Dokážte, že rovnosť |AS| . |BS| = |CS| . |AB| platí práve vtedy, keď je uhol ACB pravý.
B-I-3
Určte reálne čísla a, b, pre ktoré má sústava
x2 + y2 + 2z2 = 16
xyz2 + xy + z2 = a
x + y + 2z = b
v obore reálnych čísel práve jedno riešenie.
B-I-4
Sú dané kružnice k a l s rôznymi polomermi, ktoré sa dotýkajú
zvonku v bode T. Priesečníkom M dvoch ich spoločných dotyčníc veďme sečnicu s oboch kružníc. Označme X ten z oboch priesečníkov kružnice k so sečnicou s, ktorý je vzdialenejší od bodu M. Podobne označme Y, ten z oboch priesečníkov kružnice l so sečnicou s, ktorý
je vzdialenejší od bodu M. Nech P je taký bod, že XTYP je rovnobežník. Určte množinu bodov P zodpovedajúcich všetkým takým sečniciam s.
B-I-5
Deväťsten ABCDEFGHV vznikol zlepením kocky ABCDEFGH a pravidelného štvorbokého ihlana EFGHV. Na každú stenu tohoto deväťstena sme napísali číslo. Štyri z napísaných
čísel sú 25, 32, 50 a 57. Pre každý vrchol deväťstena ABCDEFGHV sčítame čísla na všetkých stenách, ktoré ho obsahujú. Dostaneme tak deväť rovnakých súčtov. Určte zvyšných päť čísel napísaných na stenách tohoto telesa.
B-I-6
Daný je rovnostranný trojuholník XYZ s ťažiskom T a stranou dĺžky 5 cm. Zostrojte rovnobežník ABCD s obsahom 8 cm2 a stranou AB dĺžky 2 cm tak, aby body X,
Y, Z, T ležali po rade na priamkach AB, BC, CD, DA.
| hore |
B-S-1
Pre ktoré reálne čísla a, b je funkcia
f(x) = a|x - 1| + b(x - 3) + |x - b| + x - 1
ohraničená?
B-S-2
Daná je úsečka XZ dĺžky 7 cm a jej body S, Y tak, že |XS| = 2 cm, |YZ| = 1 cm. Zostrojte pravouhlý trojuholník ABC s preponou AB tak, aby bod S bol stredom kružnice vpísanej trojuholníku ABC a body X, Y, Z ležali po rade na priamkach AC, AB, BC.
B-S-3
Do výrazu
1 - 2 + 3 - 4 + 5 - 6 + ... + 99 - 100
sme vpísali niekoľko zátvoriek tak, že nakoniec sú v každej dvojici odpovedajúcich si zátvoriek práve tri čísla a výraz neobsahuje žiadny súčin. Koľko rôznych výsledkov môžeme takto dostať?
B-II-1
Nájdite všetky reálne čísla c, pre ktoré má rovnica
(c2 + c - 8)(x + 2) - 8|x - c + 2| = c|x + c + 14|
nekonečne veľa riešení v obore celých čísel.
B-II-2
Deväťsten vznikol zlepením kocky a pravidelného štvorbokého ihlana. Na každej stene tohto deväťstena je napísané jedno číslo. Ich súčet je 3003. Pre každú stenu S uvažovaného deväťstena sčítame čísla na všetkých stenách, s ktorými má S spoločnú práve jednu hranu. Dostaneme tak deväť rovnakých súčtov. Určte všetky čísla napísané na stenách deväťstena.
B-II-3
Daný je lichobežník ABCD, v ktorom |AB| = 8 cm a |ÐABC| = 90°. Jeho obvod je 28 cm. Polkružnica k s priemerom AB sa dotýka strany CD. Vypočítajte dĺžky zvyšných strán daného lichobežníka, ak strana AB je jeho:
a) základňou,
b) ramenom.
B-II-4
Daný je obdĺžnik KLMN, |KN| > |KL|. Zostrojte rovnoramenný trojuholník ABC so základňou AB dĺžky |KL| tak, aby jeho výška va obsahovala body K, N, výška vb bod L a výška vc bod M. (Výškami tu rozumieme priamky.)
| hore |
A-I-1
Nech P(x), Q(x) sú kvadratické mnohočleny také, že čísla –22, 7, 13 sú tri z koreňov rovnice P(Q(x)) = 0. Určte štvrtý koreň tejto rovnice.
A-I-2
Nech K, L, M sú po rade vnútorné body strán BC, CA, AB daného trojuholníka ABC také, že kružnice vpísané dvojiciam trojuholníkov ABD a CAK, BCL a ABL, CAM a BCM majú
vonkajší dotyk. Potom platí
|BK| . |CL| . |AM| = |CK| . |AL| . |BM|
Dokážte.
Poznámka: Z uvedenej rovnosti vyplýva na základe Cevovej vety, že priamky AK, BL, CM prechádzajú spoločným bodom.
A-I-3
V obore kladných reálnych čísel riešte sústavu
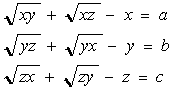
kde a, b, c sú dané kladné čísla.
A-I-4
V rovine je daných 1999 zhodných trojuholníkov s obsahom 1, ktoré sú obrazmi jedného trojuholníka v rôznych posunutiach. Ak je prienikom všetkých daných trojuholníkov
množina M, ktorá obsahuje ťažisko každého z nich, je obsah množiny M aspoň 1/9. Dokážte.
A-I-5
Daná je funkcia f : N ® N taká, že
f(n)= 1, ak je n nepárne, a f(n) = k pre každé párne číslo n = 2kl,
kde k je prirodzené číslo a l číslo nepárne. Určte najväčšie prirodzené číslo n, pre ktoré platí
f (1) + f (2) + ... + f (n) ≤ 123456
A-I-6
Daný je štvorboký ihlan ABCDV s podstavou ABCD. Jeho hrany AB, CD sú rovnobežné a roviny ABV a CDV navzájom kolmé. Označme P pätu výšky z vrcholu V na stranu AB v
trojuholníku CDV. Dokážte nerovnosť
|AV|2 + |BV|2 + |CV|2 + |DV|2 ≥ |PQ|2+ 2(SABV + SCDV + SPQV)
kde SXYZ označuje obsah trojuholníka XYZ. Zistite tiež, kedy platí rovnosť.
| hore |
A-S-1
Určte, pre ktoré reálne čísla p má sústava rovníc
(x - y)2 = p2,
x3 - y3 = 16
práve jedno riešenie v obore reálnych čísel.
A-S-2
Je daný trojuholník ABC. Vnútri jeho strán BC, CA, AB uvažujme po rade body K, L, M také, že úsečky AK, BL, CM sa pretínajú v bode U. Ak trojuholníky AMU a KCU majú obsah P a trojuholníky MBU a CLU obsah Q, potom P = Q. Dokážte.
A-S-3
Určte najmenšie prirodzené číslo k, pre ktoré platí: Ak vyberieme ľubovoľných k rôznych čísel z množiny {1, 2,, 3, ..., 2000}, tak medzi vybranými číslami existujú dve, ktorých súčet alebo rozdiel je 667.
| hore |
A-II-1
Nech P(x) je kvadratický trojčlen. Určte všetky korene rovnice
P(x2 + 4x - 7) = 0,
ak viete, že medzi nimi je číslo 1 a aspoň jeden koreň je dvojnásobný.
A-II-2
Daný je rovnoramenný lichobežník UVST, v ktorom 3|ST| < 2|UV|. Zostrojte rovnoramenný trojuholník ABC so základňou AB tak, aby body B, C ležali na priamke VS, bod U na priamke AB a bod T bol ťažiskom trojuholníka ABC.
A-II-3
Dokážte, že pre ľubovoľné kladné čísla a, b platí nerovnosť
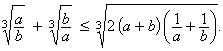
Zistite, kedy nastane rovnosť.
A-II-4
Určte všetky konvexné štvoruholníky ABCD s nasledujúcou vlastnosťou: Vnútri štvoruholníka ABCD existuje bod E taký, že každá priamka, ktorá prechádza týmto bodom a pretína strany AB a CD vo vnútorných bodoch delí štvoruholník ABCD na dve časti s rovnakým obsahom. Svoju odpoveď zdôvodnite.
| hore |
A-III-1
Nech n je prirodzené číslo. Dokážte, že súčet ![]() je deliteľný trinástimi práve vtedy, keď n je párne.
je deliteľný trinástimi práve vtedy, keď n je párne.
A-III-2
Daný je rovnoramenný trojuholník ABC so základňou AB. Na jeho výške CD je zvolený bod P tak, že kružnice vpísané trojuholníku ABP a štvoruholníku PECF sú zhodné; pritom bod E je priesečník priamky AP so stranou BC a F priesečník priamky BP so stranou AC. Dokážte, že aj kružnice vpísané trojuholníkom ADP a BCP sú zhodné.
A-III-3
V rovine je daných 2000 zhodných trojuholníkov s obsahom 1, ktoré sú obrazmi toho istého trojuholníka v rôznych posunutiach. Každý z týchto trojuholníkov obsahuje ťažiská všetkých ostávajúcich. Dokážte, že obsah zjednotenia týchto trojuholníkov je menší ako ![]() .
.
A-III-4
Pre ktoré kvadratické funkcie f(x) existuje taká kvadratická funkcia g(x), že korene rovnice g(f(x)) = 0 sú štyri rôzne po sebe idúce členy aritmetickej postupnosti a súčasne sú aj koreňmi rovnice f(x)g(x) = 0 ?
A-III-5
Monika zhotovila papierový model trojbokého ihlana, ktorého podstavou bol pravouhlý trojuholník. Keď model rozrezala pozdĺž odvesien podstavy a pozdĺž ťažnice jednej zo stien, vznikol po rozvinutí do roviny štvorec so stranou a. Určte objem tohoto ihlana.
A-III-6
Nájdite všetky štvormiestne čísla ![]() (v desiatkovej sústave), pre ktoré platí rovnosť
(v desiatkovej sústave), pre ktoré platí rovnosť
| hore |