48. ročník matematickej olympiády 1998-1999 | |||||
| Z4 | Z5 | Z6 | Z7 | Z8 | Z9 |
| 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo |
| 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo |
| 3. kolo | |||||
Z4-I-1
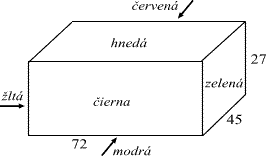
Miško mal drevený kvádrik s rozmermi 27 mm, 45 mm, 72 mm. Každú jeho stenu natrel inou farbou tak, ako vidíš na obrázku.
Skôr ako farba stačila zaschnúť, položil kváder hnedou stenou na papier, potom ho preklopil na zelenú stenu, potom na červenú,na modrú, na žltú a naposledy na červenú. Nakoniec odložil kvádrik preč a pozrel si celý obrázok. Aký obsah má zafarbená časť papiera? Aký má obvod?
Z4-I-2
Čísla 34, 52 a 18 tvoria sčítaciu rodinku, lebo súčet dvoch z nich sa rovná
tretiemu (34 + 18 = 52). Vierka si zapísala týchto 6 čísel: 267, 186, 435, 168, 453, 1074.
a) Nájdi medzi nimi všetky sčítacie rodinky.
b) Škrtni jedno z Vierkiných čísel tak, aby medzi ostatnými 5 už nebola sčítacia rodinka.
c) Aké číslo rôzne od škrtnutého môžeme k týmto piatim číslam pridať, aby po pridaní boli medzi nimi aspoň dve sčítacie rodinky? Svetlana našla štyri také čísla, nám bude stačiť, ak nájdeš dve.
Z4-I-3
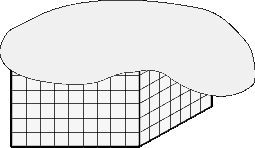
Adam má 1638 rovnako veľkých modrých a bielych kociek. Zo všetkých kociek postavil kváder, ktorého časť vidíte na obrázku.
Pritom všetky kocky vnútri sú biele a zvonka je celý kváder modrý. Koľko bielych a koľko modrých kociek má Adam?
Z4-I-4
Skočkovia po číselnom pásiku nevedia chodiť, ale len skákať. A to oboma smermi len o toľko, aké majú číslo na čapici. Kamaráti Skočkovia s číslami 14 a 18 stoja na políčku s číslom 137 a chcú doskákať na:
a) číslo 139
b) číslo 140.
Ako majú Skočkovia skákať, aby sa im to podarilo na čo najmenej skokov?
(Aby mohli spolu skákať, musí vziať jeden druhého na plecia!)

Z4-I-5
Majo vyznačil na štvorčekovom papiery tieto body:
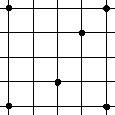
Potom začal spájať vyznačené body úsečkami tak, aby sa tieto úsečky nepretínali. Keď už nemohol žiadne dva z vyznačených bodov spojiť, skončil. Jeho traja kamaráti urobili to isté. Môže mať každý z nich iný obrázok? Nakresli tieto 4 obrázky.
Z4-I-6
Petra a Janko minuli v obchode 987 korún. Petra si kúpila plutvy a plavecké okuliare,
Janko si kúpil nafukovaciu vestu. Okuliare stáli o 178 korún menej ako
plutvy. Janko platil polovicu toho, čo Petra. Koľko korún stála najlacnejšia vec?
| ▲ hore ▲ |
Z5-I-1
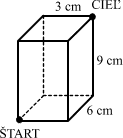
Mravce Športík a Lenítko pochodujú po hranách kvádra (obrázok). Vyšli z miesta označeného ŠTART. Lenítko si vybral najkratšiu možnú cestu do miesta označeného CIEĽ,
Športík najdlhšiu, ale ani po jednej hrane nešiel viackrát. Koľko cm prešiel Lenítko a koľko Športík?
Z5-I-2
Súčet bodiek na ľubovoľných dvoch protiľahlých stranách hracej kocky je 7. Z troch takýchto hracích kociek zlepíme teleso. (Zlepujeme vždy len 2 celé steny.) Aký najmenší počet bodiek môže mať na povrchu?
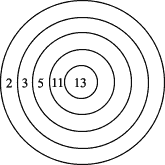
Z5-I-3
Aký najmenší počet šípov musel zasiahnuť terč na obrázku, ak je súčet nastrieľaných bodov 150?
Z5-I-4
Doplň chýbajúce členy pravidelnosti, v ktorej každý člen je súčtom predchádzajúcich dvoch:
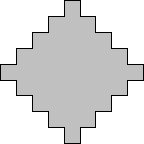
Z5-I-5
Útvar na obrázku má obsah 100 cm2. Aký najmenší obsah musel mať štvorcový papier z ktorého sme tento útvar vystrihli?
Z5-I-6
V botanickej záhrade zasadili v zime berjozku tatársku - stromček s 3 vetvičkami. Na konci každej vetvičky sa vždy na jar objaví puk, z ktorého na jeseň vyrastú 3 nové vetvičky. Mucha Bzukna v lete niektoré puky zožerie. Prvé leto zožrala Bzukna 1 puk, druhé leto 2 puky. Koľko pukov zožrala Bzukna 3. leto, ak sa na ďalšiu jar objavilo na stromčeku 29 nových pukov?
| ▲ hore ▲ |
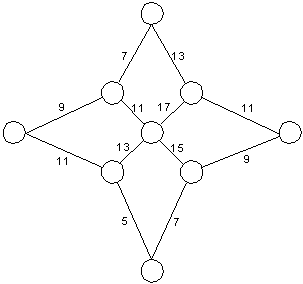
Z5-II-1
Doplňte do krúžkov čísla od 1 do 9 tak, aby sa súčet čísel v ľubovoľných dvoch susedných krúžkoch (spojených čiarou) rovnal číslu napísanému medzi nimi.
Z5-II-2
Paťo dostal na Vianoce tri rozprávkové knižky. Druhá kniha má o desať strán viac ako prvá kniha. Tretia kniha má o 10 strán menej ako prvá. Na očíslovanie všetkých strán všetkých troch kníh spotrebovali presne 115 sedmičiek. Koľko strán majú jednotlivé knihy?
Z5-II-3
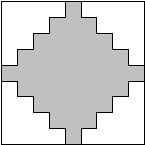
Ferko mal papier tvaru štvorca o obsahu 100 cm2. Vystrihol z neho takýto útvar: (obrázok 2). Strihal tak, aby bol útvar čo najväčší. Miško mal väčší
papier, preto ním nemusel tak šetriť. Strihal takto: (obrázok 3). Získal rovnako veľký útvar ako Ferko. Aký obsah mal Miškov papier?
 |
 |
|
obrázok 2 |
obrázok 3 |
| ▲ hore ▲ |
Z6-I-1
Aritmetický priemer 7 rôznych prirodzených čísel je 56. Tieto čísla sú všetky párne, alebo sú všetky nepárne. Aké najväčšie číslo môže byť medzi nimi?
Z6-I-2
Rodné číslo má 10 číslic. Prvé dvojčíslie rodného čísla je posledným dvojčíslím roku narodenia. Druhé dvojčíslie rodného čísla je u chlapcov určené mesiacom narodenia,
u dievčat je to mesiac narodenia zväčšený o 50. Tretie dvojčíslie je dané dňom
narodenia. Posledná štvorica čísel je zvolená tak, aby rodné číslo bolo deliteľné 11.
Koľko najviac detí sa mohlo narodiť 23.11.1998, ak každé z nich musí mať iné rodné
číslo?
Z6-I-3
Máme 4 kocky o objemoch 1, 8, 27 a 64 cm3. Aký najväčší (najmenší) povrch môže mať teleso z nich zlepené? Menšiu kocku smieme prilepiť k väčšej len celou stenou.

Z6-I-4
Jeden ufodeň má 10 ufohodín, jedna ufohodina má sto ufominút.
a) Napíšte čo ukazujú digitálne ufohodiny, ak ručičkové ukazujú (obr.)
b) Nakreslite, čo ukazujú ručičkové ufohodiny, ak digitálne ukazujú:
8:25 |
c) Ručičkové ufohodiny ukazovali 4 ufohodiny a 5 ufominút. Veľká ručička sa posunula o 9°. Aký čas ukazujú ručičkové ufohodiny teraz?
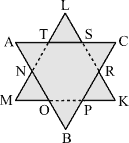
Z6-I-5
Dva rovnostranné trojuholníky ABC a KLM položíme cez seba tak,
ako je nakreslené na obrázku: KL║AB, |AT| = |CR| = |BO|.
Trojuholník ABC má obvod 237 cm, trojuholník
KLM má obvod 372 cm. Aký obvod má hviezdička ANMOBPKRCSLT?
Z6-I-6
Na troch miskách sú čerešne. Ferko zobral z prvej misky toľko čerešní, koľko bolo na druhej miske a pridal ich na druhú. Potom zobral z druhej misky toľko čerešní,
koľko bolo na tretej a pridal ich na tretiu. Nakoniec zobral z tretej misky toľko,
koľko zostalo na prvej a pridal ich na prvú. Na každej miske je teraz 16 čerešní. Koľko čerešní bolo pôvodne na 1., 2. a 3. miske?
| ▲ hore ▲ |
Z6-II-1
V záhrade rastie 8 jabloní s červenými, 3 jablone so žltými a 5 jabloní so zelenými jablkami. Minulý rok sa na jednom strome urodilo priemerne 87 kg jabĺk. Červených jabĺk nazbierali spolu 5-krát viac než žltých. Zelených nazbierali 2,5-krát menej než červených. Koľko kilogramov jabĺk sa priemerne urodilo na jednom strome s červenými jablkami? Aká bola priemerná úroda z jedného stromu so zelenými jablkami? A aká zo stromu so žltými?
Z6-II-2
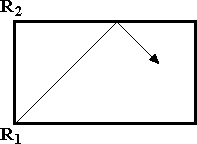
Dlhšia strana biliardového stola meria 3 m. Hráč poslal biliardovú guľu z rohu R1 pod uhlom 45°, tak ako je to naznačené na obrázku. Po troch odrazoch sa guľa dostala do rohu R2. (Guľa sa odrazí vždy pod rovnakým uhlom ako dopadne). Aká je dĺžka kratšej strany stola?
Z6-II-3
Monika nakreslila tri štvorce s celočíselnými dĺžkami strán, potom vypočítala ich obsahy. Zistila, že sú to všetko trojciferné čísla. Pri ich zapisovaní použila každú z číslic 1, 2, ..., 9 práve raz. Aké obsahy majú Monikine štvorce?
| ▲ hore ▲ |
Z7-I-1
V čisle 71 839 664 518 nahraďte niektoré cifry štvorkami tak, aby vzniklo čo najmenšie číslo deliteľné 18.
Z7-I-2
Barón Prášil rozprával: V Čudákove som dostal štvoruholníkovú oplátku. Jedným priamym rezom som ju rozdelil na 3 (čo do obsahu) rovnako veľké diely. Vieš takú oplátku narysovať (urob), alebo si barón Prášil vymýšľal?
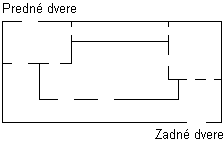
Na obrázku je plán začarovaného domu. Vstúpime doň prednými dverami. Každé dvere, ktorými prejdeme, sa za nami zatvoria a zamknú. Mohlo by sa stať, že zostaneme uväznení v niektorej zamknutej miestnosti?
Z7-I-4
Malý Mikuláš chcel telefonovať babičke, ktorá býva na druhom konci mesta. Zabodol však telefónne číslo. Pamätal si, že
Nájdite pre Mikuláša babičkine telefónne číslo. |
Číselník telefónu: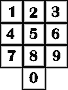 |
Z7-I-5
Stroj na výrobu radu čísel funguje takto: vytlačí nulu, jednotku, a ďalej vždy od predposledného zapísaného čísla odpočíta posledné zapísané číslo, vytlačí znamienko a poslednú číslicu výsledku. Vytlačenie každého čísla (aj so znamienkom) trvá 1 sekundu. Stroj naprogramujeme tak, aby sa zastavil
a) po vytlačení trojice čísel,z ktorých ani jedno nie je záporné,
b) po vytlačení trojice 0, -1, 2,
c) po vytlačení trojice 1, 2, 3.
Ako dlho bude stroj v jednotlivých prípadoch pracovať?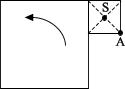
Z7-I-6
Narysujte celú dráhu, ktorú opíše vrchol A a stred S malého štvorca pri preklápaní malého štvorca po celom obvode veľkého štvorca. Strana veľkého štvorca meria 9 cm, obsah malého štvorca je deväťkrát menší než obsah veľkého štvorca.
| ▲ hore ▲ |
Z7-II-1
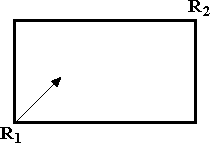
Päťnásobok šírky biliardového stola sa rovná trojnásobku jeho dĺžky. Hráč vyslal biliardovú guľu pod uhlom 45° z rohu R1, tak ako je to naznačené na obrázku. Kým sa guľa prvý krát odrazila od okraja, prešla dráhu dlhú 168 cm. Koľko metrov meria celá dráha, ktorú guľa prejde od rohu R1, kým dorazí do rohu R2? Načrtni dráhu gule.
Z7-II-2
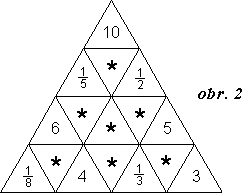
V trojuholníku na obr. 2 nahraďte hviezdičky tak, aby platilo:
d = a . b . c podľa obr. 1
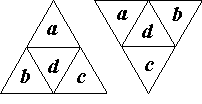 obr. 1 |
 |
Z7-II-3
Bratia kúpili svojim rodičom k striebornej svadbe tieto darčeky: 11 pohárov, 7 hrnčekov, 6 tanierikov, 5 súprav posteľnej bielizne, 3 police a 2 lampy. Na účtenke z obchodu sú tieto ceny: 231, 180, 2210, 6513, 143, 3002.
Zistite cenu jedného kusu z každého druhu tovaru.
Koľko synov mali rodičia, ak každý z nich prispel na nákup rovnakým dielom?
(Za každý druh tovaru je na účtenke uvedená iba jeho celková cena a jednotkové ceny za kus každého tovaru sú celé čísla.)
| ▲ hore ▲ |
Z8-I-1
Je daná nekonečná pravidelnosť čísel 1, 2, 4, 8, 16, 32, ...
a) Akou číslicou končí číslo, ktoré je v tejto pravidelnosti na 1998. mieste?
b) Má nejaké číslo v tejto pravidelnosti ciferný súčet 1998?
c) Vidíme, že súčet prvých troch čísel je deliteľný siedmimi. Dá sa nájsť trojica po sebe idúcich čísel pravidelnosti, ktorá nie je deliteľná 7? Vysvetlite.
Z8-I-2
Drôtený štvorec sme stlačením zdeformovali na kosoštvorec tak, že jedna jeho uhlopriečka sa predĺžila o 40%. O koľko percent sa skrátila druhá uhlopriečka?
Z8-I-3
Nájdite všetky trojciferné prvočísla abc s ciframi
a, b, c, pre ktoré platí: dvojciferné čísla ab, ac, ba, bc, ca, cb sú tiež prvočísla.
Z8-I-4
Nájdite všetky štvorciferné desatinné čísla, ktoré majú túto vlastnosť: Ak odčítame od mysleného štvorciferného desatinného čísla jeho zrkadlový obraz, dostaneme číslo 62,73. (číslo 27,5 je trojciferné a jeho zrkadlový obraz je 5,72.)
Z8-I-5
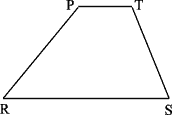
Na obrázku je daný lichobežník PRST. Zostrojte trojuholník ABC ak vieme, že bod P je stred strany AB a bod T je stred strany BC. Body S, R ležia na niektorých z priamok AB, BC, CA.
Z8-I-6
Je daný pravidelný štvorboký ihlan ABCDV. Jeho steny sú čerstvo natreté farbou. Uhol AVB má veľkosť 67,5° a bočné hrany majú dĺžku 4 cm. Ihlan položíme na jednu z bočných stien a začneme ho preklápať okolo bočných hrán, pričom vrchol V ostáva na mieste a bočné steny zanechávajú farebnú stopu.
a) Narysujte hranicu najväčšej možnej zafarbenej plochy.
b) Narysujte hranicu najväčšej možnej zafarbenej plochy, ak je natretá len jedna bočná stena ihlana.
c) Narysujte hranicu najväčšej možnej zafarbenej plochy, ak sú natreté dve bočné steny ihlana.
| ▲ hore ▲ |
Z8-II-1
V autobuse je 45 miest na sedenie. Na prvej zastávke nastúpilo do prázdneho autobusu niekoľko cestujúcich. ![]() z nich zostala stáť, ostatní obsadili
z nich zostala stáť, ostatní obsadili ![]() všetkých sedadiel. Na druhej zastávke niekoľko cestujúcich vystúpilo, ale pristúpilo toľko ďalších, že obsadili všetky miesta na sedenie a stáť zostala rovnaká časť všetkých cestujúcich ako predtým. Určte, koľko cestujúcich pristúpilo na druhej zastávke, ak viete, že len
všetkých sedadiel. Na druhej zastávke niekoľko cestujúcich vystúpilo, ale pristúpilo toľko ďalších, že obsadili všetky miesta na sedenie a stáť zostala rovnaká časť všetkých cestujúcich ako predtým. Určte, koľko cestujúcich pristúpilo na druhej zastávke, ak viete, že len ![]() všetkých cestujúcich, ktorí nastúpili na prvej alebo druhej zastávke, cestovala z prvej zastávky na tretiu zastávku alebo ďalej.
všetkých cestujúcich, ktorí nastúpili na prvej alebo druhej zastávke, cestovala z prvej zastávky na tretiu zastávku alebo ďalej.
Z8-II-2
Drôtený model štvorca bol zdeformovaný stlačením na kosoštvorec tak, že jedna jeho uhlopriečka sa predĺžila o 20 %. Určte pomer obsahov kruhov vpísaných do vytvoreného kosoštvorca a pôvodného štvorca.
Z8-II-3
Budeme hovoriť, že číslo p je podriadené číslu v (t.j. v je jeho veliteľom),
ak súčet čísla p a jeho ciferného súčtu sa rovná v. Napríklad číslo 17 je podriadené číslu 25 (t.j. číslo 25 je veliteľo čísla 17), pretože 17 + 1 + 7 = 25.
Zistite, či čísla 26 a 97 sú veliteľmi niektorých čísel. Môže mať niektorý dvojciferný veliteľ viac podriadených? Ak áno, uveďte príklad takého veliteľa.
| ▲ hore ▲ |
Z9-I-1
Nájdite všetky šesťciferné desatinné čísla, ktoré majú túto vlastnosť:
Ak odčítame od mysleného šesťciferného desatinného čísla jeho zrkadlový obraz, dostaneme číslo 883,602. (Číslo 27,5 je trojciferné a jeho zrkadlový obraz je 5,72.)
Z9-I-2
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú na stranách AB, BC, CA dané po rade dvojice bodov K, L a M, N a O, P tak,že
|AK| = |LB| = 1/4 |AB| , |BM| = |NC| = 1/4 |BC| , |CO| = |PA| = 1/4 |CA|.
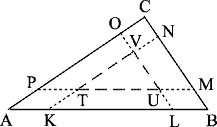
Priamky KN, MP, OL ohraničujú trojuholník TUV s celočíselnými
dĺžkami strán. Obsah S trojuholníka TUV je S = 6 cm2. Určite obvod trojuholníka ABC.
Z9-I-3
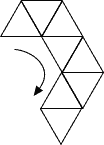
Na každej stene pravidelného štvorstena je jedno z čísel 5, 9, 13, 17. Štvorsten položíme na hrací plán pozostávajúci z rovnostranných trojuholníkov zhodných so
stenami štvorstena a preklápame ho po pláne v smere šípky (obrázok).
Pritom sčítavame čísla, ktoré ležia vždy na spodnej stene štvorstena. Ako treba postaviť štvorsten na plán, aby bol tento súčet maximálny?
Z9-I-4
Janko býva na tej istej strane ulice, ako je škola, do ktorej chodí. Cestou do školy sčítaval čísla domov, okolo ktorých išiel. Začal číslom domu, v ktorom býva. Keď
bol súčet 99, prešiel cez prvú priečnu ulicu a začal sčítavať odznova. Pri prechode cez ďalšiu priečnu ulicu bol súčet 117 a Janko začal opäť sčítavať od začiatku. Keď prišiel ku škole, dostal (aj s číslom školy) súčet 235. Aké je číslo domu, v ktorom Janko býva, a aké číslo má škola?
Na jednej strane ulice sú domy číslované za sebou idúcimi párnymi, na druhej strane ulice za sebou idúcimi nepárnymi číslami.
Z9-I-5
Dva nezhodné rovnoramenné trojuholníky majú rovnaký obsah, ich obvody sa líšia
o 2 cm. Dĺžky ramien oboch trojuholníkov sú 5 cm. Určite dĺžky základní týchto trojuholníkov.
Z9-I-6
V jedálni bol veľký hrniec so 7 litrami presladeného a malý hrniec s 3 litrami málo
sladkého čaju. Do jednej kanvice sme nabrali presladený a do druhej rovnaké množstvo málo sladkého čaju. Presladený čaj z kanvice sme celý vyliali do malého hrnca a málo sladký čaj z kanvice sme celý naliali do veľkého hrnca. V oboch hrncoch je teraz rovnako sladký čaj. Koľko čaju sme naberali do kanvíc?
| ▲ hore ▲ |
Z9-II-1
Ochrancovia prírody sadili stromčeky. Keby ich sadili tak, aby v každom rade bol rovnaký počet stromčekov, boli by zasadili 684 stromčekov. Keby ich sadili tak, aby v každom párnom rade bolo o jeden stromček menej, bolo by ich 675. Pritom počet radov v oboch prípadoch je rovnaký. Koľko stromčekov je v dlhšom rade?
Z9-II-2
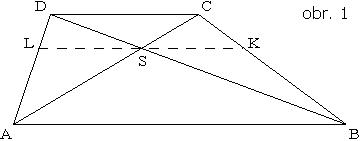
V lichobežníku ABCD platí: |AB| = 12 cm a |CD| = 6 cm. Nech S je priesečník uhlopriečok lichobežníka a priamka p prechádzajúca bodom S je rovnobežná so základňou AB lichobežníka. Priamka p pretína úsečky BC, DA v bodoch K, L (viď obr.1). Určte dĺžku úsečky KL.
Z9-II-3
Nájdite prvočísla p, r, ktoré sú riešeniami rovnice: p + p2 + p3 + r + r2 + r3 = 2393
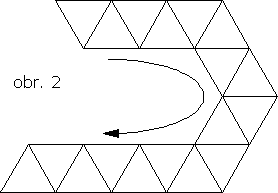
Z9-II-3
Každá stena pravidelného štvorstena je označená iným jednociferným číslom. Pri prevalovaní štvorstena po hracom pláne (viď obr.2) sme sčítali čísla na stenách, ktoré sa dotkli plánu. Po prevalení štvorstena na posledné políčko plánu bol súčet 132. Určte všetky možnosti, ako mohol byť štvorsten popísaný číslami.
| ▲ hore ▲ |
Z9-III-1
Nájdite všetky prirodzené čísla x, y také, že x2 + y2 = aaa.
Poznámka: aaa je trojciferné číslo s rovnakými ciframi.
Z9-III-2
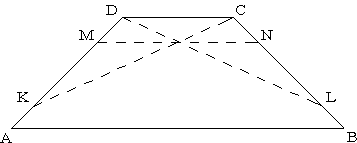
Je daný rovnoramenný lichobežník ABCD s výškou v = 20 cm a ramenom b = 25 cm. Na ramenách BC, DA sú po rade body L, N a M, K tak, že |AK| = |MD| = |LB| = |NC| = ![]() |AD|. Úsečky KC a DL sa pretínajú v bode úsečky MN (obr.1). Určite dĺžky základní lichobežníka ABCD a jeho obvod a obsah.
|AD|. Úsečky KC a DL sa pretínajú v bode úsečky MN (obr.1). Určite dĺžky základní lichobežníka ABCD a jeho obvod a obsah.
 obr.1
obr.1
Z9-III-3 |
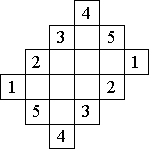 obr.2 |
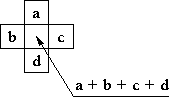 obr.3 |
Z9-III-4
Štvoruholníku ABCD s vnútornými uhlami s veľkosťami α, β, γ, δ je vpísaná kružnica k. Body dotyku kružnice k a strán AB, BC, CD, DA sú vrcholy štvoruholníka KLMN, ktorý má tiež vnútorné uhly s veľkosťami α, β, γ, δ (nemusia byť v tomto poradí). Určte veľkosti α, β, γ, δ.
| ▲ hore ▲ |